Zadanie 9: Zbadaj przebieg zmienności funkcji
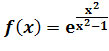 i naszkicuj jej wykres.
i naszkicuj jej wykres.Rozwiązanie:
1. Wyznaczamy dziedzinę funkcji.
Przez 0 dzielimy, zatem mianownik
![]() .
.
Czyli
![]() .
.
Stąd
![]() .
.
Zatem
![]()
D(f) = (![]() , -1)
, -1)
![]() (-1, 1)
(-1, 1)
![]() (1,
(1,
![]() )
=
)
=
![]() \ {-1, 1}.
\ {-1, 1}.
2. Obliczamy granice na końcach dziedziny.
Granice przy zmiennej z dążącej do plus i minus nieskończoności obliczamy w ten sposób, że dzielimy ułamek przez najwyższą potęgę zmiennej z mianownika.
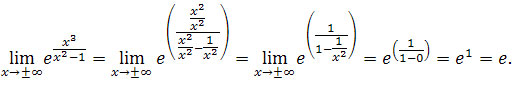
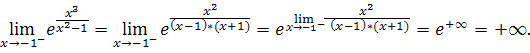
Powyższą granicę obliczyliśmy w ten sposób, że najpierw wstawiliśmy -1 za zmienną
x, otrzymaliśmy wyrażenie
![]() co oznacza, że granicą jest wartość
co oznacza, że granicą jest wartość
![]() ,
lub
,
lub
![]() , w celu
określenia znaku wartości granicy wstawiamy za zmienną x wartość
troszkę mniejszą od -1 (gdyż liczymy granicę z lewej strony punktu -1)
na przykład -1,1 i otrzymujemy wartość dodatnią, co oznacza, że
granicą jest wyrażenie {
, w celu
określenia znaku wartości granicy wstawiamy za zmienną x wartość
troszkę mniejszą od -1 (gdyż liczymy granicę z lewej strony punktu -1)
na przykład -1,1 i otrzymujemy wartość dodatnią, co oznacza, że
granicą jest wyrażenie {
![]() }, czyli
}, czyli
![]() .
.