Zadanie 3: Ile wyrazów ma ciąg arytmetyczny, którego wyrazy spełniają następujący układ równań:
Rozwiązanie:
Ponieważ ciąg 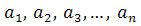 jest ciągiem arytmetycznym o
różnicy r, to jego podciąg, ciąg
jest ciągiem arytmetycznym o
różnicy r, to jego podciąg, ciąg![]() jest również ciągiem
arytmetycznym i jego różnica jest równa 2r. (Zauważmy, że
jeśli
jest również ciągiem
arytmetycznym i jego różnica jest równa 2r. (Zauważmy, że
jeśli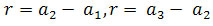 ,
czyli
,
czyli
![]() ,
to
,
to
![]() )
)
Ponieważ sumę n pierwszych wyrazów ciągu 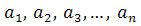 wyrażamy wzorem postaci
wyrażamy wzorem postaci
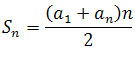 ,
gdzie a1 jest pierwszym wyrazem ciągu, an
jest n-tym wyrazem ciągu, to sumę n pierwszych wyrazów
ciągu
,
gdzie a1 jest pierwszym wyrazem ciągu, an
jest n-tym wyrazem ciągu, to sumę n pierwszych wyrazów
ciągu ![]() obliczamy ze wzoru postaci
obliczamy ze wzoru postaci
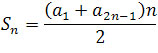 ,
gdzie a1 jest pierwszym wyrazem ciągu, a2n-1
ostatnim wyrazem ciągu. (Zauważmy, że ciąg
,
gdzie a1 jest pierwszym wyrazem ciągu, a2n-1
ostatnim wyrazem ciągu. (Zauważmy, że ciąg ![]() ma n wyrazów) Wracając do układu równań mamy
ma n wyrazów) Wracając do układu równań mamy
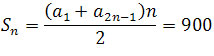
Zatem
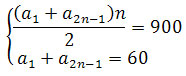
Z drugiego równania wstawiamy a1 + a2n-1 do pierwszego równania i otrzymujemy
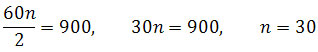
Odpowiedź: Ciąg arytmetyczny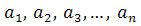 , którego wyrazy spełniają układ równań
, którego wyrazy spełniają układ równań
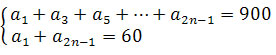 ma 30 wyrazów.
ma 30 wyrazów.