Zadanie 12: Czy można wyznaczyć liczbę rzeczywistą a taką, aby funkcja określona wzorem
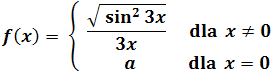 była ciągła w
punkcie
była ciągła w
punkcie
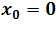 ? Odpowiedź uzasadnić.
? Odpowiedź uzasadnić.Rozwiązanie:
Skorzystamy z warunku ciągłości funkcji w punkcie
![]() postaci
postaci
![]() , mamy
, mamy ![]() .
.
Pokażemy, że nie istnieje granica
![]() , w tym
celu policzymy
, w tym
celu policzymy ![]() i
i
![]() oraz stwierdzimy, że
oraz stwierdzimy, że
![]() , (co dowiedzie, że
granica
, (co dowiedzie, że
granica
![]() nie
istnieje).
nie
istnieje).
Obliczamy ![]() ,
korzystamy ze wzoru
,
korzystamy ze wzoru ![]() dla dowolnej liczby rzeczywistej, mamy
dla dowolnej liczby rzeczywistej, mamy
![]()
Ponieważ liczymy
granicę przy x dążącym do punktu 0 z lewej strony, czyli zbliżamy się do 0 wartościami
ujemnymi, zatem wartość bezwzględną możemy opuścić z minusem, korzystamy
również ze wzoru z teorii granic postaci
 , mamy
, mamy
![]()
Czyli ![]()