Supermatma.pl

Zadanie 1: Obliczyć granicę ciągu o wyrazie ogólnym
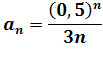
Rozwiązanie:

Ciąg (a_n) jest iloczynem dwóch ciągów, ciągu geometrycznego c_n = (0,5)ⁿ i ciągu .

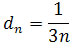Ciąg d_n na mocy twierdzenia (jeśli jest liczbą rzeczywistą, to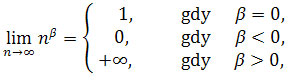) jest zbieżny do 0,

ciąg c_n = (0,5)ⁿ jest ciągiem geometrycznym o ilorazie
q = 0,5 (-1, 1), zatem jego granica jest równa 0.

Wykorzystując twierdzenie: Jeśli ciąg (a_n) ma granicę a, a ciąg (b_n) ma granicę b (gdzie a, b są liczbami rzeczywistymi), to ciąg  (a_n * b_n) ma granicę a * b,  mamy

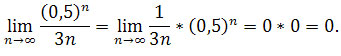
Sposób 2: Obliczając granicę ciągu (a_n) wystarczy zauważyć, że licznik jest ciągiem geometrycznym o ilorazie q = 0,5(-1, 1), czyli jego granica jest równa 0, a mianownik dąży do , zatem ciąg (a_n) jest zbieżny do 0.