Supermatma.pl

Zadanie 2: Obliczyć granicę .

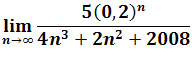Rozwiązanie:

Sposób 1:

Licznik Ciągu (a_n) geometrycznym o ilorazie
q = 0,2 (-1, 1), czyli jego granica jest równa 0, a mianownik dąży do , zatem ciąg (a_n)) jest zbieżny do 0.

Sposób 2:

Ciąg (a_n) jest iloczynem dwóch ciągów, ciągu geometrycznego c_n = (0,2)ⁿ o ilorazie q = 0,2 (-1, 1), którego granica jest równa 0 i ciągu .

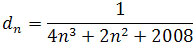Obliczając granicę ciągu d_n dzielimy licznik i mianownik przez najwyższą potęgę zmiennej n z mianownika, czyli przez n³, mamy