Supermatma.pl

Zadanie 6: Obliczyć granicę .
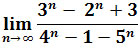Rozwiązanie:

Dzielimy licznik i mianownik przez ciąg geometryczny o największym ilorazie występującym w mianowniku, czyli przez 5ⁿ mamy

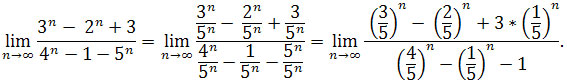
Ciągi 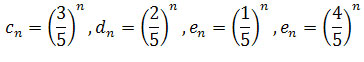są zbieżne do 0 ponieważ są ciągami geometrycznymi o ilorazach równych odpowiednio .

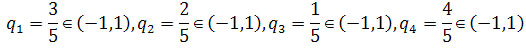Stosując twierdzenie: Jeśli ciąg (a_n) ma granicę a, a ciąg (b_n) ma granicę b (gdzie a, b są liczbami rzeczywistymi), to

a) ciąg  (a_n + b_n) ma granicę a + b;

b) ciąg  ma granicę 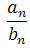,  o ile b 0.

Mamy

.
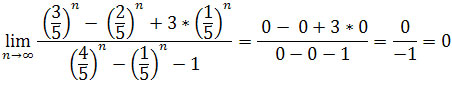