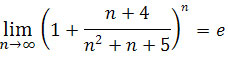Supermatma.pl
MATEMATYKA
WITAMY W SERWISIE |
Zadanie 4: Obliczyć granicę
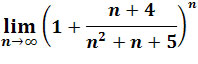 .
.Rozwiązanie:
Przekształcamy ciąg do postaci, w której będziemy mogli
skorzystać ze wzoru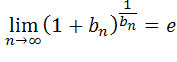 ,
jeśli
,
jeśli
![]() . Szukamy takiego x dla którego
. Szukamy takiego x dla którego
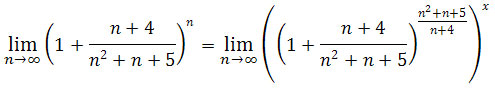 .
.
Czyli
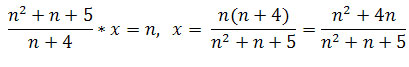 .
.
Zatem/p>
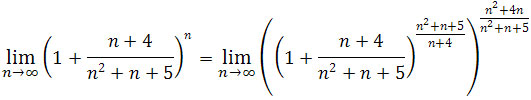 .
.
Korzystając ze wzoru 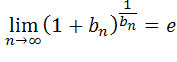 ,
jeśli
,
jeśli
![]() otrzymujemy
otrzymujemy
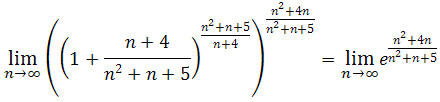 .
.
Zatem wystarczy policzyć granicę
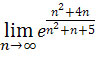 .
Dzielimy licznik i mianownik wyrażenia w potędze przez najwyższą potęgę
zmiennej n z mianownika, czyli przez n2 otrzymujemy
.
Dzielimy licznik i mianownik wyrażenia w potędze przez najwyższą potęgę
zmiennej n z mianownika, czyli przez n2 otrzymujemy
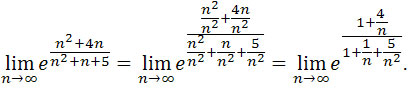
Ciągi
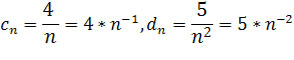 na mocy twierdzenia, jeśli
na mocy twierdzenia, jeśli
![]() jest liczbą rzeczywistą, to
jest liczbą rzeczywistą, to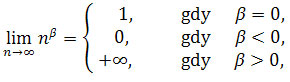 są
zbieżne do 0. Zatem
są
zbieżne do 0. Zatem
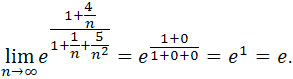
Czyli