Supermatma.pl

Zadanie 7: Obliczyć granicę .
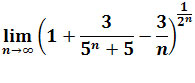Rozwiązanie:

Sprowadźmy ułamki do wspólnego mianownika

.

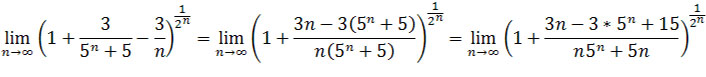Zanim przekształcimy wyraz ogólny naszego ciągu do postaci, w której będziemy mogli skorzystać ze wzoru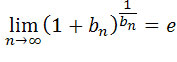, jeśli sprawdzimy, czy granicą ciągu 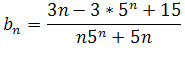jest liczba 0.

Podzielimy licznik i mianownik ciągu (b_n) przez taki wyraz, aby granicą wyrażenia w mianowniku była liczba skończona różna od zera, czyli podzielimy licznik i mianownik przez 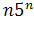mamy

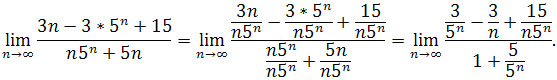
Ciąg 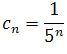jest zbieżny do 0, gdyż jest ciągiem geometrycznym o ilorazie .

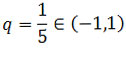Ciąg 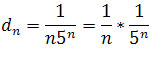jest zbieżny do 0, gdyż jest iloczynem ciągów zbieżnych do 0. Zatem

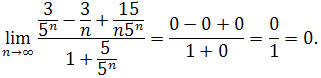
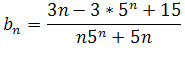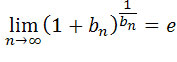Czyli granicą ciągu jest liczba 0, przekształcimy teraz nasz ciąg do postaci, w której będziemy mogli skorzystać ze wzoru, jeśli , w tym celu szukamy takiego x dla którego

.

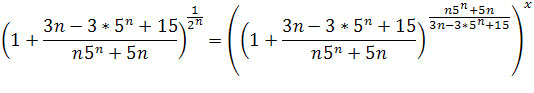Czyli

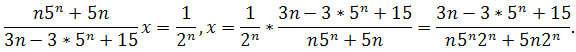
Zatem

.

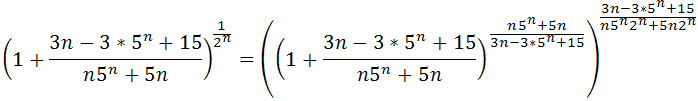Korzystając ze wzoru 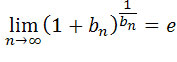 , jeśli otrzymujemy

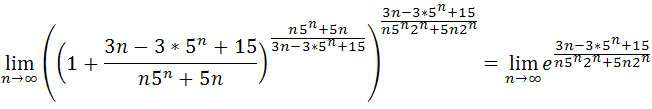
Zatem wystarczy policzyć granicę .

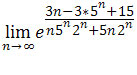Dzielimy licznik i mianownik przez taki wyraz, aby granicą wyrażenia w mianowniku była liczba skończona różna od zera, czyli podzielimy licznik i mianownik przez mamy

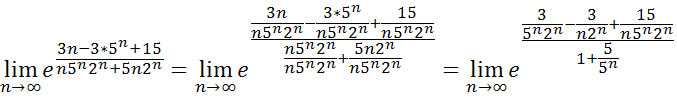
Ciąg 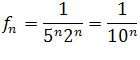  jest zbieżny do 0, gdyż jest ciągiem geometrycznym o ilorazie .

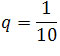Ciągi 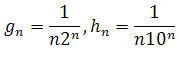są zbieżne do 0, gdyż są iloczynami ciągów zbieżnych do 0.

Zatem

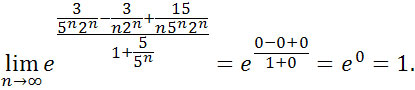
Czyli