Supermatma.pl

Zadanie 13: Obliczyć granicę ciągu .
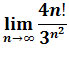Rozwiązanie:
 

Obliczając granicę posłużymy się następującym twierdzeniem

Twierdzenie: Jeżeli dla ciągu (a_n) zachodzi 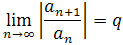 , gdzie q jest stałą wówczas

                     a) gdy q < 1, to ,

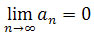                     b) gdy q > 1, to

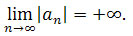
Ponieważ wszystkie wyrazy ciągu 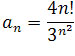są dodatnie to wartość bezwzględną możemy opuścić, mamy

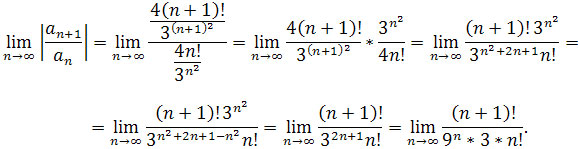
Korzystając z definicji n! = n * (n-1) * (n-2) * ... * 2 * 1, czyli n! = n * (n-1)!, otrzymujemy

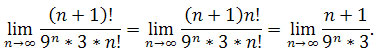
Dzielimy licznik i mianownik przez taki wyraz, aby granicą w wyrażenia w mianowniku była liczba skończona różna od 0, czyli dzielimy przez 9ⁿ otrzymujemy

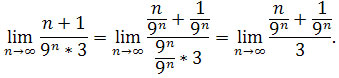
Ciąg 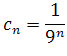jest zbieżny do 0, ponieważ jest ciągiem geometrycznym o ilorazie równym  .

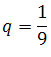Pokażemy, że granicą ciągu 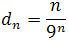jest liczba 0.

Obliczamy

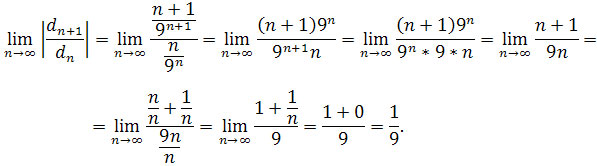
Zatem 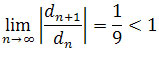, stosując twierdzenia przytoczone na początku zadania mamy .

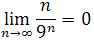Wracając do ciągu (a_n) mamy

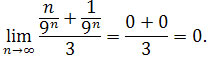
Czyli 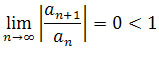, na mocy twierdzenia przytoczonego na początku zadania mamy