Supermatma.pl

 
Zadanie 5: Obliczyć granicę .
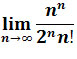Rozwiązanie:

Obliczając granicę ciągu (a_n) posłużymy się następującym twierdzeniem

Twierdzenie: Jeżeli dla ciągu (a_n) zachodzi 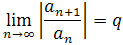 , gdzie q jest stałą wówczas

                     a) gdy q < 1, to ,

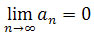                     b) gdy q > 1, to

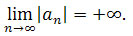
Ponieważ wszystkie wyrazy ciągu są dodatnie to wartość bezwzględną możemy opuścić, mamy

Korzystając z definicji n! = n * (n-1) * (n-2) * ... * 2 * 1, czyli n! = n * (n-1)!, otrzymujemy

Wykorzystując wzór   mamy

Czyli , zatem na na mocy twierdzenia, jeżeli dla ciągu (a_n) zachodzi 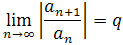 ,   gdzie q jest stałą i q > 1, to

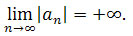
Mamy