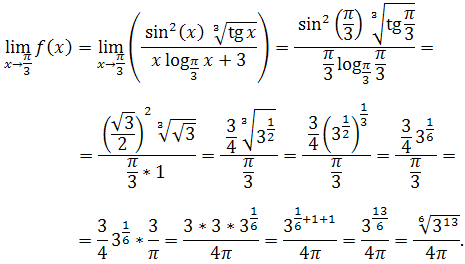Zadanie 2: Wykorzystując definicję Heinego granicy funkcji, obliczyć granicę funkcji
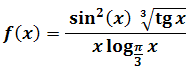 w
punkcie
w
punkcie
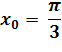 .
.Rozwiązanie:
Bierzemy dowolny ciąg
![]() taki,
że
taki,
że
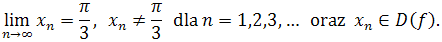
Zatem zgodnie z definicją Heinego ( granicy funkcji ), obliczenie granicy funkcji ![]() w punkcie
w punkcie
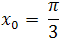 sprowadza się do obliczenia granicy ciągu
sprowadza się do obliczenia granicy ciągu
![]() , gdy
n dąży do + .
, gdy
n dąży do + .
( Czyli zamiast liczyć granicę
![]() wystarczy policzyć granicę
wystarczy policzyć granicę
![]() .)
.)
Korzystając z twierdzeń z teorii granic ciągów, mamy
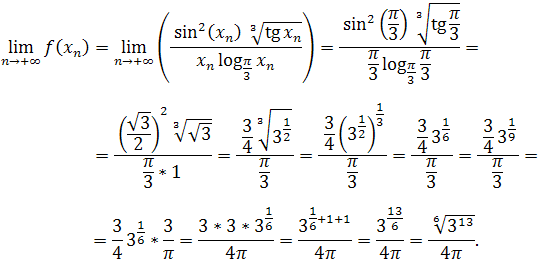
Obliczając granicę funkcji
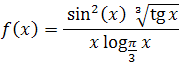 w punkcie
w punkcie
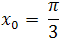 wstawiamy
wstawiamy
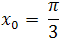 do funkcji
do funkcji ![]() i otrzymujemy
i otrzymujemy