Zadanie 2: Obliczyć granicę funkcji
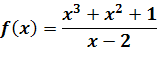 w punkcie
w punkcie
Rozwiązanie:
Obliczamy ![]() . Wstawiamy
. Wstawiamy ![]() do wyrażenia
do wyrażenia 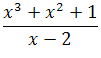 i otrzymujemy
i otrzymujemy 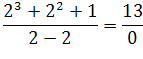 .
Co oznacza, że granica
.
Co oznacza, że granica ![]() może być równa
może być równa
![]() ,
,
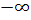 , lub może wcale nie
istnieć.
, lub może wcale nie
istnieć.
Przypomnijmy, że granica (właściwa, lub niewłaściwa) ![]() istnieje wtedy i tylko wtedy, gdy
istnieje wtedy i tylko wtedy, gdy ![]() .
Wówczas
.
Wówczas ![]() .
.
Obliczamy ![]() .
Jak pokazaliśmy wstawiając
.
Jak pokazaliśmy wstawiając ![]() do wyrażenia
do wyrażenia 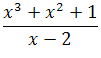 otrzymujemy
otrzymujemy 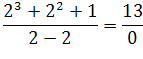 .
.
Zatem granica ![]() jest równa
jest równa
![]() ,
,
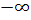 .
.
W celu określenia znaku granicy, badamy znaki licznika i mianownika.
Licznik wynosi 13, czyli jest zawsze większy od 0.