Zadanie 6: Zbadaj przebieg zmienności funkcji
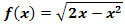 i naszkicuj jej wykres.
i naszkicuj jej wykres.Rozwiązanie:
1. Wyznaczamy dziedzinę funkcji.
Ponieważ pod pierwiastkiem kwadratowym mogą być tylko liczby nieujemne,
zatem
![]() .
.
Znajdujemy punkty, w których wyrażenie x * (2 - x) przyjmuje wartość 0, mamy
x * (2 - x) = 0 dla
x = 0 i x = 2. Zatem mamy do zbadania 3 przedziały: (![]() ,
0), (0, 2), (2,
,
0), (0, 2), (2,
![]() ).
).
Badamy znak w przedziale (![]() ,
0), wybieramy dowolną liczbę z przedziału (
,
0), wybieramy dowolną liczbę z przedziału (![]() ,
0),
np. -1 i wstawiamy ją do równania x * (2 - x), mamy (-1) * (2 -
(-1)) = -3 < 0.
Stąd x * (2 - x)
< 0
dla x
,
0),
np. -1 i wstawiamy ją do równania x * (2 - x), mamy (-1) * (2 -
(-1)) = -3 < 0.
Stąd x * (2 - x)
< 0
dla x
![]() (
(![]() , 0).
, 0).
Badamy znak w przedziale (0, 2), wybieramy dowolną liczbę z przedziału (0, 2),
np. 1 i wstawiamy ją do równania x * (2 - x), mamy 1 * (2 -
1) = 2 > 0.
Stąd x * (2 - x) > 0
dla x
![]() (0, 2).
(0, 2).
Badamy znak w przedziale (2, ![]() ),
wybieramy dowolną liczbę z przedziału (2,
),
wybieramy dowolną liczbę z przedziału (2,
![]() )),
np. 3 i wstawiamy ją do równania x * (2 - x), mamy 3 * (2 -
33) = -3 < 0.
Stąd x * (2 - x)
< 0
dla x
)),
np. 3 i wstawiamy ją do równania x * (2 - x), mamy 3 * (2 -
33) = -3 < 0.
Stąd x * (2 - x)
< 0
dla x
![]() (2,
(2,
![]() ).
).
Sprawdzamy, że f(0) = 0 ,f(2)=0.
Zatem
![]() dla
x
dla
x
![]() [0, 2].
[0, 2].
Stąd D(f) = [0, 2].