Zadanie 9: Zbadaj przebieg zmienności funkcji
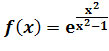 i naszkicuj jej wykres.
i naszkicuj jej wykres.Rozwiązanie, strona 5:
6. Wyznaczenie przedziałów monotoniczności i ekstremów funkcji .
Badam warunek konieczny istnienia ekstremum funkcji, czyli sprawdzam dla
jakich punktów z dziedziny funkcji
![]() pochodna tej
funkcji zeruje się.
pochodna tej
funkcji zeruje się.
![]()
![]() -2x =0
. Stąd
-2x =0
. Stąd
![]() dla x = 0.
dla x = 0.
Badamy warunek dostateczny istnienia ekstremum funkcji f(x) w punkcie x = 0.
![]()
![]() -2x > 0.
Stąd
-2x > 0.
Stąd
![]() dla x
< 0
dla x
< 0
![]()
![]() -2x < 0.
Stąd
-2x < 0.
Stąd![]() dla x
> 0
dla x
> 0
Zatem w punkcie x = 0 pochodna funkcji
![]() zmienia znak z plusa na minus, zatem w punkcie x = 0 warunek
dostateczny istnienia ekstremum jest spełniony, czyli funkcja
zmienia znak z plusa na minus, zatem w punkcie x = 0 warunek
dostateczny istnienia ekstremum jest spełniony, czyli funkcja
![]() ma w punkcie x = 0 maksimum lokalne.
ma w punkcie x = 0 maksimum lokalne.
7. Wyznaczanie asymptot funkcji.
Jak obliczyliśmy w punkcie 2.) granica lewostronna funkcji
![]() w punkcie x = -1 jest równa
w punkcie x = -1 jest równa
![]() , czyli funkcja
, czyli funkcja
![]() ma w punkcie x = -1 lewostronną asymptotę pionową, granica prawostronna funkcji
ma w punkcie x = -1 lewostronną asymptotę pionową, granica prawostronna funkcji
![]() w punkcie x = 1 jest równa
w punkcie x = 1 jest równa
![]() , czyli funkcja
, czyli funkcja
![]() ma w punkcie 1 prawostronną asymptotę pionową.
ma w punkcie 1 prawostronną asymptotę pionową.