Ekstremum funkcji

Teoria. (Strona 5)

Stwierdzenie: Jeżeli funkcja jest określona i różniczkowalna na pewnym otoczeniu   punktu 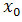, gdzie i jeśli , to w punkcie 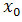funkcja

a) ma minimum,  jeśli   dla i  dla ,

b) ma maksimum, jeśli   dla i  dla .

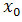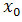Czyli funkcja określona i różniczkowalna w otoczeniu punktu ma ekstremum w punkcie jeśli jeśli pochodna funkcji w punkcie 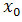jest równa 0 i pochodna funkcji przy przejściu przez punkt 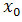zmienia znak:

a) z plusa na minus, to mamy maksimum,

  b) z minusa na plus to mamy minimum.      

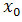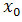Załóżmy, że funkcja ma w pewnym otoczeniu punktu pierwszą pochodną oraz istnieje druga pochodna funkcji w punkcie , to możemy sformułować drugi warunek dostateczny istnienia ekstremum w punkcie .

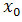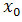Drugi warunek dostateczny: (Znak drugiej pochodnej funkcji w punkcie podejrzanym o ekstremum.)  Jeśli druga pochodna funkcji w punkcie podejrzanym o ekstremum jest jest ciągła i dodatnia , to funkcja ma w punkcie minimum, jeśli natomiast , to funkcja   ma w punkcie 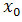maksimum.