Supermatma.pl

Zadanie 12: Obliczyć granicę ciągu .
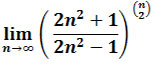Rozwiązanie:

Zauważmy, że

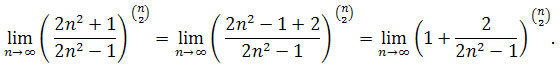
Korzystając ze wzoru tzw. współczynnika Newtona postaci 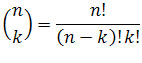,  gdzie k = 0,1,2, ..., n  , n 5 £, mamy , 

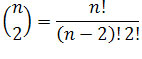Wykorzystując definicję silni

n! = n * (n-1) * (n-2) * ... * 2 * 1,

czyli n! = n * (n-1)!,  n! = n * (n-1) * (n-2)!

otrzymujemy

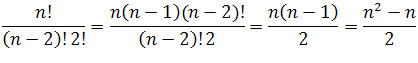
Zatem

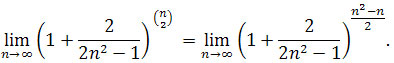
Przekształcimy powyższą granicę do postaci, w której będziemy mogli skorzystać ze wzoru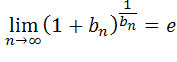, jeśli . Szukamy takiego x dla którego

.

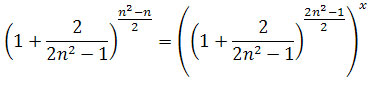Czyli

 .

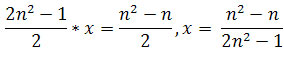Zatem

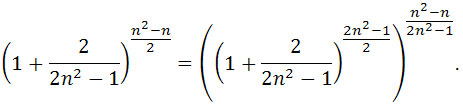
Korzystając ze wzoru 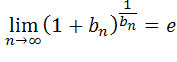 , jeśli otrzymujemy

.

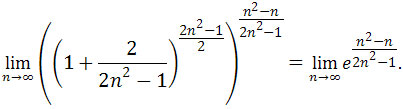Zatem wystarczy policzyć granicę .

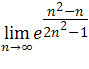Dzielimy licznik i mianownik wyrażenia w potędze przez zmienną n o najwyższej potędze z mianownika, czyli dzielimy przez n² otrzymujemy

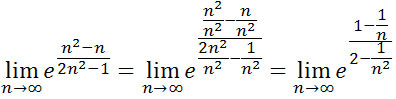
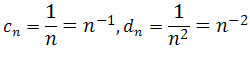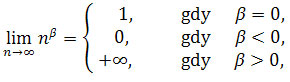Ciągi na mocy twierdzenia, jeśli jest liczbą rzeczywistą, tosą zbieżne do 0. Zatem

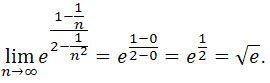
Czyli