Supermatma.pl

Zadanie 6: Obliczyć granicę .
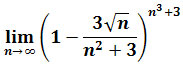Rozwiązanie:

Przekształcamy ciąg do postaci, w której będziemy mogli skorzystać ze wzoru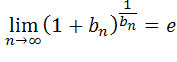, jeśli . Szukamy takiego x dla którego

.

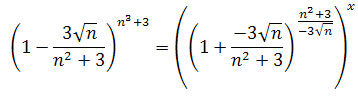Czyli

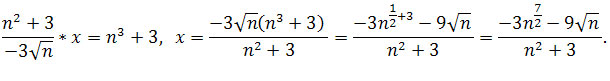  Zatem

.

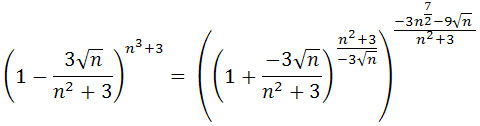Korzystając ze wzoru 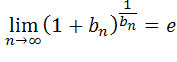 , jeśli otrzymujemy

.

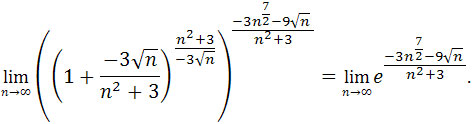Zatem wystarczy policzyć granicę 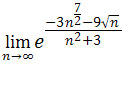. Wyłączamy w liczniku wykładnika potęgi zmienną n o najwyższej potędze występującą w liczniku wykładnika, czyli wyłączamy , Wyłączamy w mianowniku wykładnika potęgi zmienną n o najwyższej potędze występującą w mianowniku, czyli n² mamy

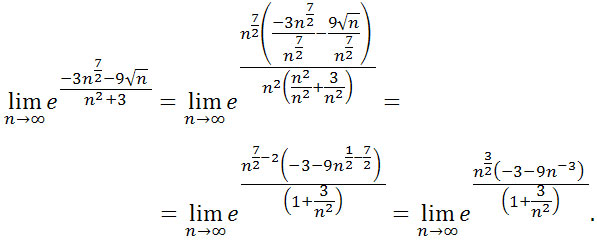
Ciągi 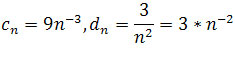na mocy twierdzenia, jeśli jest liczbą rzeczywistą, to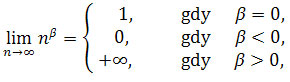są zbieżne do 0. Ciąg 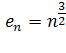na mocy tego samego twierdzenia jest rozbieżny do . Zatem

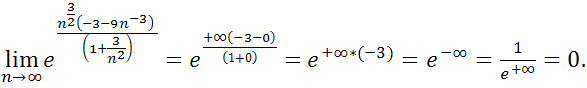
Czyli