Supermatma.pl

 
Zadanie 5: Obliczyć granicę .
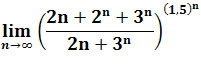Rozwiązanie:

Zauważmy, że

Przekształcamy nasz ciąg do postaci, w której będziemy mogli skorzystać ze wzoru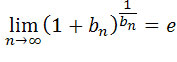, jeśli . Szukamy takiego x dla którego

.

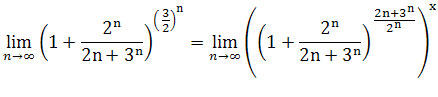Czyli

 .

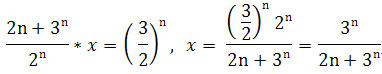Zatem

.

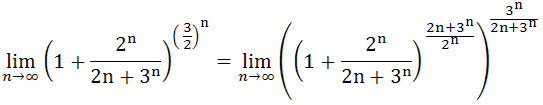Sprawdzimy, czy możemy wykorzystać wzór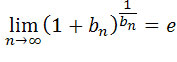, jeśli , w tym celu policzymy granicę ciągu 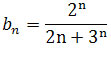. Dzielimy licznik i mianownik przez 3ⁿ mamy

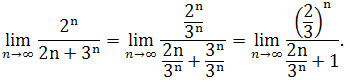
Ciąg 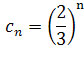jest zbieżny do 0, ponieważ jest ciągiem geometrycznym o ilorazie ,

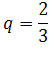Ciąg 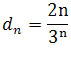jest zbieżny do 0 na mocy wzoru 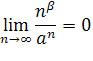  , dla a > 1, zatem

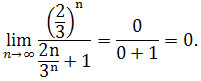
Przypomnijmy

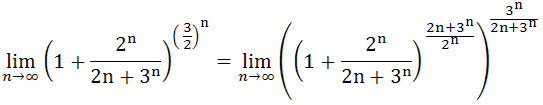
Wewnątrz nawiasu w wykładniku potęgi jest ciąg 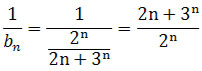który jest odwrotnością ciągu 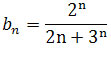, oraz jak policzyliśmy , zatem możemy stosować wzór

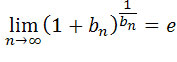, jeśli otrzymujemy

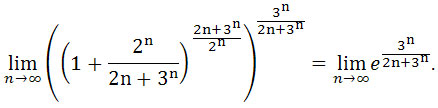
Zatem wystarczy policzyć granicę .

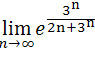Dzielimy licznik i mianownik wyrażenia w potędze przez 3ⁿ.

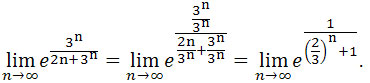
Ciąg 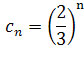jest zbieżny do 0, ponieważ jest ciągiem geometrycznym o ilorazie .

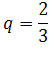Zatem

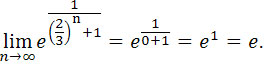
Czyli