Supermatma.pl
MATEMATYKA
WITAMY W SERWISIE |
Ekstremum funkcji.
Zadanie 1: Znaleźć ekstrema funkcji
.Rozwiązanie:
Zadanie 2: Dla jakiej wartości parametru a funkcja dana wzorem
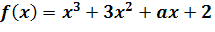ma minimum lokalne w punkcie x = 1.Rozwiązanie:
Zadanie 3: Znajdź ekstrema funkcji zadanej wzorem
.Rozwiązanie:
Zadanie 4: Wyznacz długości boków prostokąta o stałym obwodzie 2p tak, aby przekątna tego prostokąta była najkrótsza.
Rozwiązanie:
Zadanie 5: Liczba dodatnia a jest sumą trzech liczb, z których jedna jest równa 10, Wyznaczyć, pozostałe dwie liczby, aby iloczyn wszystkich trzech liczb był największy.
Rozwiązanie:
Zadanie 6: Który z walców o danej objętości V ma najmniejsze pole powierzchni całkowitej.
Rozwiązanie:
Zadanie 7: Jaka powinna być długość podstawy trapezu, aby jego pole powierzchni było największe, jeśli długość każdego z pozostałych boków jest równa 10 cm.
Rozwiązanie:
Zadanie 8: Pole powierzchni trójkąta równoramiennego wpisanego w okrąg o promieniu R = 2 jest funkcją odległości podstawy trójkąta od środka okręgu, określić tę funkcję wzorem i wyznaczyć jej maksimum.
Rozwiązanie:
Zadanie 9: Wykazać, że następujące funkcja dana wzorem
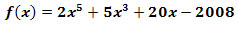nie ma ekstremum.Rozwiązanie:
Zadanie 10: Znajdź ekstrema funkcji
Rozwiązanie:
Zadanie 11: Znajdź ekstrema lokalne funkcji
.Rozwiązanie:
Zadanie 12: Znaleźć ekstremum lokalne funkcji danej wzorem
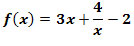w przedziale
x
[1, 8].Rozwiązanie:
Zadanie 13: Udowodnij, że zachodzi nierówność ln x ² x - 1 dla x > 0.
Rozwiązanie:
Zadanie 14: Rozważmy wszystkie czworokąty wpisane w okrąg, których jeden bok jest średnicą tego okręgu, a dwa kolejne boki mają równe długości. Wyznaczyć ten spośród rozważanych czworokątów, który ma największe pole.
Rozwiązanie: